알고리즘의 시간 복잡도 분석
좀더 빠른 알고리즘을 만들기 위해선 알고리즘의 속도를 측정할 수 있어야 한다.
두 알고리즘의 속도를 비교하는 직관적인 방법은 해당 알고리즘으로 프로그램을 구현한 뒤 수행시간을 측정하는 것이다.
이 경우 외부요인(하드웨어, OS, Compiler, 문자열 구현방식, 함수 인자의 전달방식)으로 정확하게 측정할 수 없다.
그렇다면 수행시간을 측정하는 방법은 무엇이 있을까?
반복문이 지배한다.
수행시간을 반복문으로 비교 할 수 있다.
for문 O(N) | 이중 for문 -> O(N^2) | 3중 for문 O(N^3) 등등
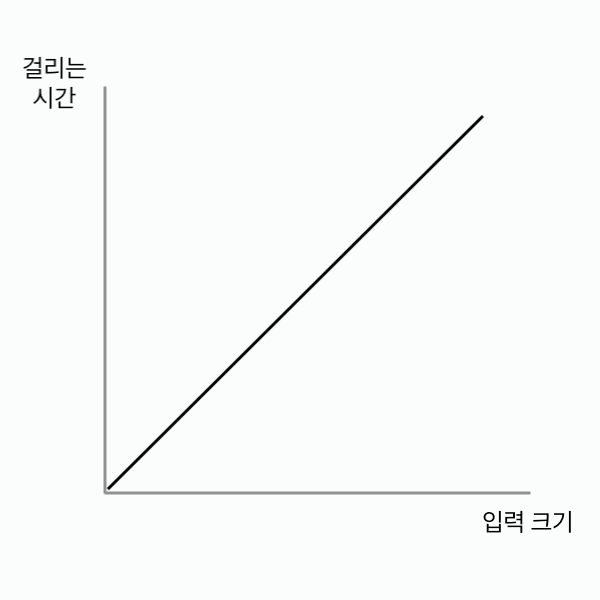
선형 시간 알고리즘
입력크기에 비례해 시간이 선형으로 증가하는 알고리즘 O(N^2)
Example Codes
n부터 m까지 순회하면서 value를 찾는 코드
int sequentialSearch(int array[], int n, int m, int value) { // Starts from n to m
int i;
for (i = n; i <= m; i++)
if (array[i] == value)
return i;
return -1;
}이동 평균을 구하는 선형 시간 알고리즘
Stack<Double> movingAverage1(Stack<Double> a, int m){
Stack<Double> stack = new Stack<Double>();
int n = a.size();
for(int idx = m-1; idx < n; ++idx) {
// list[idx]까지의 이동 평균 값을 구하라.
double partialSum = 0;
for(int sidx = 0; sidx < m; ++idx) {
partialSum += a.get(idx - sidx).doubleValue();
stack.push(partialSum / n);
}
}
return stack;
}
선형 이하 시간 알고리즘
이진 탐색 알고리즘
입력값이 단계가 지날때마다 n/2씩 줄어드는 알고리즘 O(log2N)
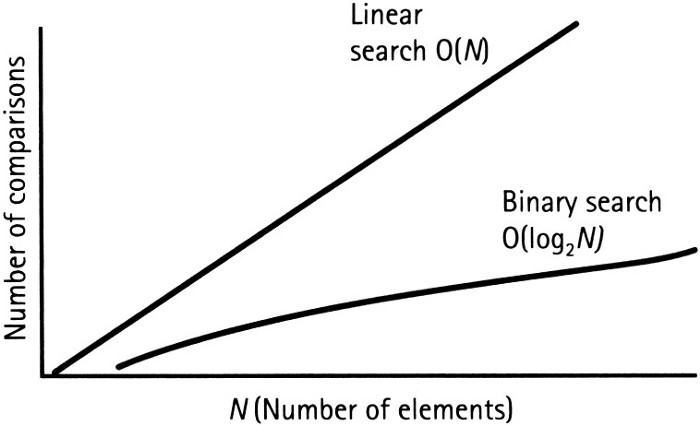
ex) Up Down 게임 / 전화번호부에서 전화번호 찾기 등등
Example Code
주어진 배열의 인덱스를 찾는 이진 탐색 알고리즘
class BinarySearchExample{
public static void binarySearch(int arr[], int first, int last, int key){
int mid = (first + last)/2;
while( first <= last ){
if ( arr[mid] < key ){
first = mid + 1;
}else if ( arr[mid] == key ){
System.out.println("Element is found at index: " + mid);
break;
}else{
last = mid - 1;
}
mid = (first + last)/2;
}
if ( first > last ){
System.out.println("Element is not found!");
}
}
public static void main(String args[]){
int arr[] = {10,20,30,40,50};
int key = 30;
int last=arr.length-1;
binarySearch(arr,0,last,key);
}
}지수 시간 알고리즘
다항 시간 알고리즘
변수 N과 N^2, 그 외 N의 거듭제곱들의 선형 결합으로 이루어진 식들을 다항식이라 한다.
반복문의 수행 횟수를 입력 크기의 다항식으로 표현할 수 있는 알고리즘을 다항 시간 알고리즘이라 한다.
지수 시간 알고리즘
N이 하나 증가할 때마다 걸리는 시간이 배로 증가하는 알고리즘 2^N을 지수 시간 알고리즘이라 한다.
Example Code
M의 사람이 모두 먹을 수 있는 경우의 수를 구하는 알고리즘 (N * M * 2^M)
static final int INF = 987654321;
boolean canEverybodyEat(Stack<Integer> menu) {
return true;
}
static int M;
int selectMenu(Stack<Integer> menu, int food) {
// 기저 사례: 모든 음식에 대해 만들지 여부를 결정했을 때
if (food == M) {
if (canEverybodyEat(menu))
return menu.size();
// 아무것도 먹지 못하는 사람이 있을 경우
return INF;
}
// 이 음식을 만들지 않는 경우의 답을 계산
int ret = selectMenu(menu, food + 1);
menu.push(food);
ret = Math.min(ret, selectMenu(menu, food + 1));
menu.pop();
return ret;
}소인수 분해의 수행 시간 ( 입력의 크기에 대해 지수 시간이 걸림 )
// 자연수 n의 소인수 분해 결과를 담은 정수 배열을 반환한다.
Stack<Integer> factor(int n){
Stack<Integer> stack = new Stack<Integer>();
if(n == 1) {
stack.add(1);
return stack;
// n == 1인 경우 예외로
}
for(int div = 2; n > 1; ++div) {
while(n % div == 0) {
n /= div;
stack.push(div);
}
}
return stack;
}
시간 복잡도
시간복잡도란?
시간복잡도(time complexity)란 가장 널리 사용되는 알고리즘의 수행 시간 기준
알고리즘이 실행되는 동안 수행하는 기본적인 연산의 수를 입력의 크기에 대한 함수로 표현한 것
기본적인 연산이란 더 작게 쪼갤 수 없는 최소 크기의 연산
최소 크기 연산 예제
1. 두 부호 있는 32비트 정수의 사칙연산
2. 두 실수형 변수의 대소 비교
3. 한 변수에 다른 변수 대입하기
최소 크기 연산이 아닌것들 ( 반복문을 포함 )
1. 정수 배열 정렬하기
2. 두 문자열이 서로 같은지 확인하기
3. 입력된 수 소인수 분해하기
시간복잡도가 낮다고 해서 항상 더 빠르게 동작하는 것은 아니다.
입력의 크기가 작을때는 시간 복잡도가 높은 알고리즘이 더 빠르게 작동할 수도 있다.
입력의 크기가 커지면 커질수록 시간 복잡도가 낮은 알고리즘이 효율적이게 된다.
수행 시간 어림짐작하기
계산 복잡도 클래스: P, NP, NP-완비
References By
알고리즘 문제 해결 전략
프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략, 구종만 지음, 인사이트, ISBN 978-89-6626-054-6 새 소식 책 소개 <알고리즘 문제 해결 전략>은 새로운 알고리즘 책입니다. 종이에 적힌 의사코드
book.algospot.com
순차 검색 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 순차 검색 알고리즘(sequential search algorithm), 또는 선형 검색 알고리즘(linear search algorithm)은 리스트에서 특정한 값을 찾는 알고리즘의 하나다. 이것은 리스트에서
ko.wikipedia.org
https://medium.com/@jacolam/binary-searches-9f0e90e52eff
Binary Searches
The binary search is the most popular search algorithm due to its efficiency . Given an list of a billion items, the binary search would…
medium.com
'Algorithm > 개념 정리' 카테고리의 다른 글
| [알고리즘 문제 해결 전략] 1. 문제 해결 시작하기 (0) | 2022.12.04 |
|---|---|
| [알고리즘 문제 해결 전략] 시작하기 (0) | 2022.12.04 |
| 클래스란? (0) | 2022.11.11 |
| 배열 복제하기 (0) | 2022.11.11 |
| 소수 나열하기 (0) | 2022.11.11 |