LinkedList의 head와 끝에서 n번째의 노드의 위치를 가지고 n번째의 노드를 지우고 list를 반환
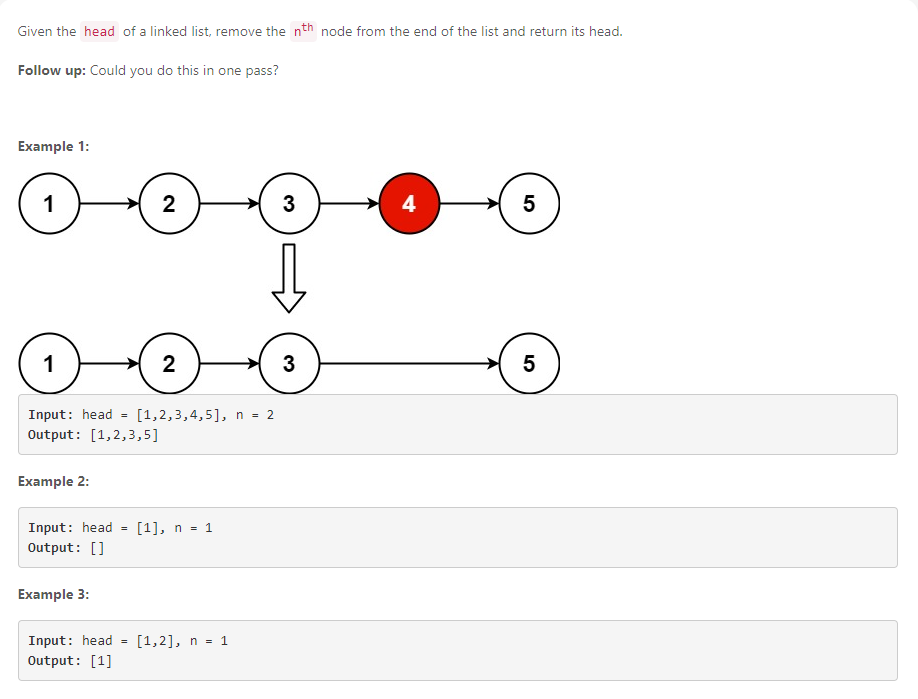
1차 시도
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
int listSize = 0;
// 순회하면서 list의 길이를 알아내기
listSize = getListSize(head, listSize) - n;
//n번째의 값 갈아끼우기
for(int i = 1; i < listSize; i++) {
head = head.next;
}
head.next = head.next.next;
return head;
}
public int getListSize(ListNode head, int listSize) {
while(head != null) {
listSize++;
head = head.next;
}
return listSize;
}
}
time complexity -> O(2N) -> O(N)
Input: [1,2,3,4,5] 2
Output: [3,5]
Expected: [1,2,3,5]
2차 - 추가적인 ListNode를 생성해서 덮어 씌우는 방식으로 해보자
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = head;
int listSize = 0;
// 순회하면서 list의 길이를 알아내기
listSize = getListSize(dummy, listSize) - n;
System.out.println(listSize);
//n번째의 값 갈아끼우기
for(int i = 1; i < listSize; i++) {
dummy = dummy.next;
}
dummy.next = dummy.next.next;
return head;
/*
dummy -> [3] -> [5];
head -> [1] -> [2] -> [3] -> [5]
*/
}
public int getListSize(ListNode dummy, int listSize) {
while(dummy != null) {
listSize++;
dummy = dummy.next;
}
return listSize;
}
}
ex1 통과
ex2 실패3차 - node가 하나인 경우 예외 케이스 만들어 주면 되나
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = head;
int listSize = 0;
// 순회하면서 list의 길이를 알아내기
listSize = getListSize(dummy, listSize) - n;
if(listSize == 0) {
head = null;
return head;
}
//n번째의 값 갈아끼우기
for(int i = 1; i < listSize; i++) {
dummy = dummy.next;
}
dummy.next = dummy.next.next;
return head;
/*
dummy -> [3] -> [5];
head -> [1] -> [2] -> [3] -> [5]
*/
}
public int getListSize(ListNode dummy, int listSize) {
while(dummy != null) {
listSize++;
dummy = dummy.next;
}
return listSize;
}
}
error case
Input: [1,2] 2
Output: []
Expected: [2]
4차 - 예외 케이스 작성
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = head;
int listSize = 0;
int target = 0;
// 순회하면서 list의 길이를 알아내기
listSize = getListSize(dummy, listSize);
target = listSize - n;
// 예외 케이스 node가 하나 있을 경우
if(listSize == 1 && target == 0) {
head = null;
return head;
} else if(listSize > 1 && target == 0) {
// [1,2] 2
dummy = dummy.next;
return dummy;
}
//n번째의 값 갈아끼우기
for(int i = 1; i < target; i++) {
dummy = dummy.next;
}
dummy.next = dummy.next.next;
return head;
/*
target = 0
-> for문 못들어감
2 = null
-> return 1
but expected 2
if(target == 0 && 1 < listSize)
*/
}
public int getListSize(ListNode dummy, int listSize) {
while(dummy != null) {
listSize++;
dummy = dummy.next;
}
return listSize;
}
}
Runtime: 0 ms
Memory Usage: 36.9 MB
getListSize -> O(N)
갈아끼우기 -> O(N)
time Complexity -> O(2N) -> O(N)
space Complexity -> O(1) (dummy)
Solution

public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
int length = 0;
ListNode first = head;
while (first != null) {
length++;
first = first.next;
}
length -= n;
first = dummy;
while (length > 0) {
length--;
first = first.next;
}
first.next = first.next.next;
return dummy.next;
}
Complexity Analysis
Time complexity : O(L)O(L).
The algorithm makes two traversal of the list,
first to calculate list length LL and second to find the (L - n)(L−n) th node.
There are 2L-n2L−n operations and time complexity is O(L)O(L).
Space complexity : O(1)O(1).
We only used constant extra space.Approach 2: One pass algorithm
Algorithm
The above algorithm could be optimized to one pass. Instead of one pointer, we could use two pointers. The first pointer advances the list by n+1 steps from the beginning, while the second pointer starts from the beginning of the list. Now, both pointers are exactly separated by n nodes apart. We maintain this constant gap by advancing both pointers together until the first pointer arrives past the last node. The second pointer will be pointing at the nth node counting from the last. We relink the next pointer of the node referenced by the second pointer to point to the node's next next node.

public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode first = dummy;
ListNode second = dummy;
// Advances first pointer so that the gap between first and second is n nodes apart
for (int i = 1; i <= n + 1; i++) {
first = first.next;
}
// Move first to the end, maintaining the gap
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
Complexity Analysis
Time complexity : O(L)O(L).
The algorithm makes one traversal of the list of LL nodes.
Therefore time complexity is O(L)O(L).
Space complexity : O(1)O(1).
We only used constant extra space.'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode] - Palindrome Linked List (0) | 2021.05.08 |
|---|---|
| [LeetCode] - Merge Two Sorted Lists (0) | 2021.05.05 |
| [LeetCode] - Delete Node in a Linked List (0) | 2021.05.03 |
| [LeetCode] - Binary Tree Level Order Traversal (0) | 2021.04.29 |
| [LeetCode] - Symmetric Tree (0) | 2021.04.29 |