분할 정복 알고리즘의 대표적 예제 중 하나인 병합 정렬은 효율적이고 범용적인 정렬 알고리즘이다.
병합 정렬 알고리즘을 구현하는 방법에는 위에서 아래로 또는 아래에서 위로 두 가지가 있습니다.
여기서는 재귀를 사용하여 자연스럽게 구현할 수있는 하향식 접근 방식을 설명합니다 .
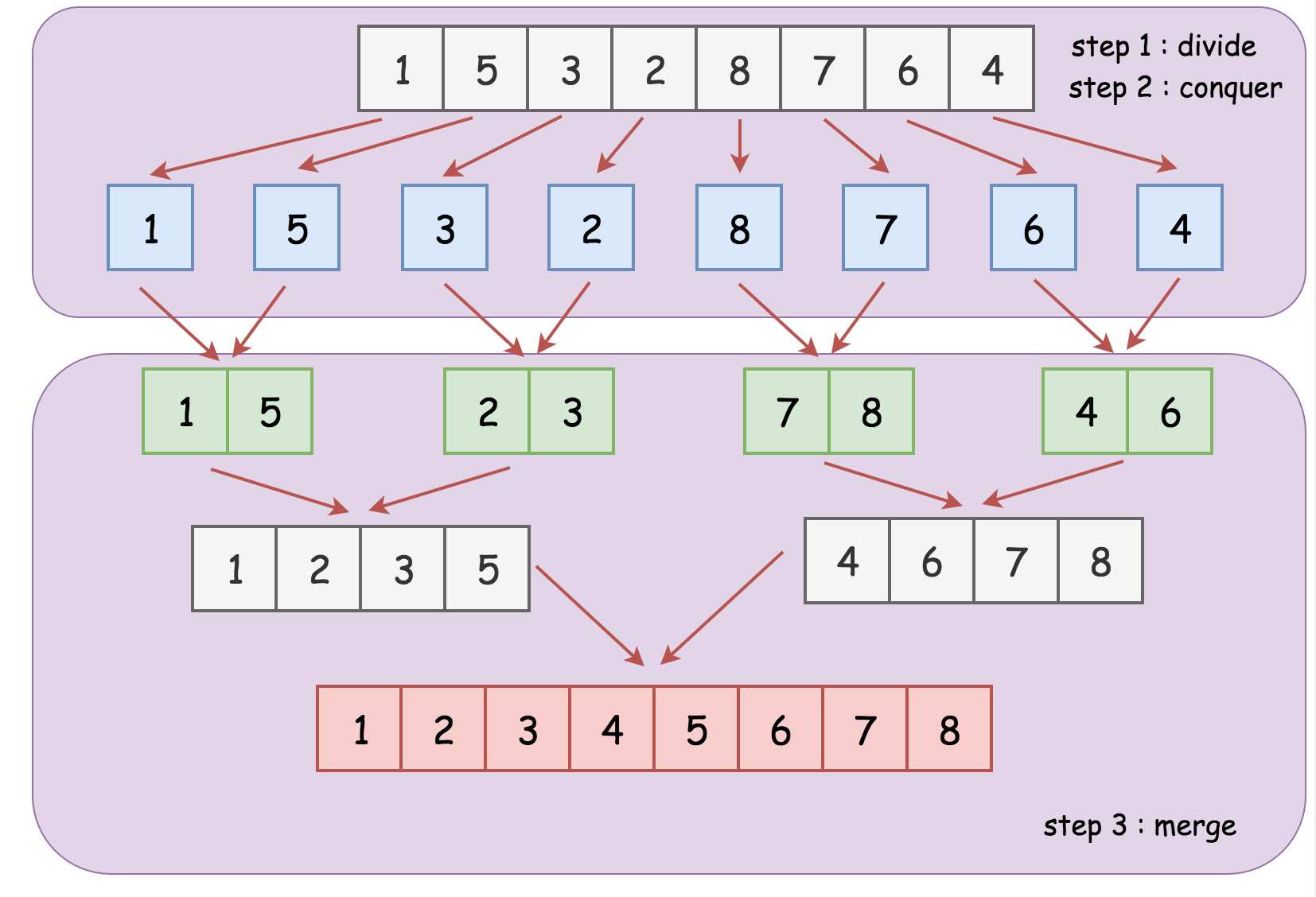
병합 정렬 알고리즘은 모든 나누기 및 정복 알고리즘과 같이 세 단계로 나눌 수 있습니다.
- 주어진 정렬되지 않은 목록을 여러 하위 목록으로 나눕니다. ( 나누기 )
- 각 하위 목록을 재귀 적으로 정렬합니다. ( 정복 )
- 정렬 된 하위 목록을 병합하여 새 정렬 된 목록을 생성합니다. ( 결합 )
하향식 접근 방식
하향식 병합 정렬 알고리즘이 어떻게 작동하는지 구체적인 예를 살펴 보겠습니다.
아래 그림과 같이 8 개의 요소가있는 정렬되지 않은 목록이 제공됩니다.
작업은 목록을 오름차순으로 정렬하는 것입니다.

- 첫 번째 단계에서는 목록을 두 개의 하위 목록으로 나눕니다. ( 나누기 )
- 그런 다음 다음 단계 에서 이전 단계의 하위 목록을 재귀 적으로 정렬합니다. ( 정복 )
- 마지막으로 위 단계에서 정렬 된 하위 목록을 반복적으로 병합하여 정렬 된 요소의 최종 목록을 얻습니다. ( 결합 )
단계 (2) 의 재귀 는 입력 목록이 비어 있거나 단일 요소를 포함하는 기본 케이스에 도달합니다 (위 그림에서 파란색으로 표시된 노드 참조).
이제 문제를 병합 문제로 줄였습니다.
이 문제는 훨씬 더 간단합니다.
두 개의 정렬 된 목록 병합은 선형 시간 복잡도로 수행 할 수 있습니다.
시간 복잡도는 O(N), N은 병합할 두 List의 총 길이입니다.
다음과 같이 병합 프로세스의 예를 보여줍니다.
다음은 하향식 병합 정렬 알고리즘의 샘플 구현입니다.

import java.util.Arrays;
public class Solution {
public int [] merge_sort(int [] input) {
if (input.length <= 1) {
return input;
}
int pivot = input.length / 2;
int [] left_list = merge_sort(Arrays.copyOfRange(input, 0, pivot));
int [] right_list = merge_sort(Arrays.copyOfRange(input, pivot, input.length));
return merge(left_list, right_list);
}
public int [] merge(int [] left_list, int [] right_list) {
int [] ret = new int[left_list.length + right_list.length];
int left_cursor = 0, right_cursor = 0, ret_cursor = 0;
while (left_cursor < left_list.length &&
right_cursor < right_list.length) {
if (left_list[left_cursor] < right_list[right_cursor]) {
ret[ret_cursor++] = left_list[left_cursor++];
} else {
ret[ret_cursor++] = right_list[right_cursor++];
}
}
// append what is remain the above lists
while (left_cursor < left_list.length) {
ret[ret_cursor++] = left_list[left_cursor++];
}
while (right_cursor < right_list.length) {
ret[ret_cursor++] = right_list[right_cursor++];
}
return ret;
}
}
상향식 접근 방식
상향식 접근 방식, 일단 하나의 요소의 하위 목록으로 목록을 나눕니다. 그런 다음 각 하위 목록이 이미 정렬되어 있습니다. 그런 다음이 시점부터 단일 목록이 남을 때까지 한 번에 두 개의 하위 목록을 병합합니다.
아래 그림에서 상향식 접근 방식이 어떻게 작동하는지 보여줍니다.
상향식 접근 방식은 반복적으로 구현할 수 있습니다.
직접 구현해보십시오 휴먼!
복잡성
병합 정렬 알고리즘 의 전체 시간 복잡성 은 다음과 같습니다. O(N log N), N은 입력 List의 길이입니다. 복잡성을 계산하기 위해 다음 단계로 분류합니다.
- 단일 요소가있는 하위 List이 남을 때까지 입력 목록을 두 개의 하위 List로 재귀 적으로 나눕니다. 이 분할 단계는 각 하위 목록의 중간 점을 계산합니다. 이는 O(1)의 시간이 걸립니다. Single Element가 남을 때까지 이 단계는 반복하면 총 시간 복잡도는 O(N)
- 그런 다음 하나의 목록이 남을 때까지 하위 목록을 반복적으로 병합합니다. 위의 그림 1 또는 그림 2 의 재귀 트리는 반복이 어떻게 반복되는지 시각화하는 데 유용합니다. 재귀 트리에서 볼 수 있듯이 각 레벨에는 N개의 elements 가 있습니다. 따라서의 O(N)이 병합 프로세스가 각 수준에서 완료되는 데 걸리는 시간입니다. 그리고 총 log N개의 레벨이 있기에 병합 프로세스의 전반적인 복잡성은 O(N log N)
병합 정렬 알고리즘에서 위 두 부분의 복잡성을 고려하여 병합 정렬의 전체 시간 복잡성은 다음과 같다고 결론을 내립니다. O(N log N)
병합 정렬 알고리즘 의 공간 복잡성 은 다음과 같습니다. O(N), N은 병합 프로세스의 각 라운드에서 병합 결과를 보관하기 위해 버퍼와 하위 목록을 유지해야하므로 입력 목록의 길이입니다.
leetcode.com/explore/learn/card/recursion-ii/470/divide-and-conquer/2868/
Account Login - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
en.wikipedia.org/wiki/Merge_sort
Merge sort - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search A divide and combine sorting algorithm In computer science, merge sort (also commonly spelled as mergesort) is an efficient, general-purpose, and comparison-based sorting algorithm. Mo
en.wikipedia.org
'Algorithm > 개념 정리' 카테고리의 다른 글
| 시간 복잡도 (Time Complexity) (0) | 2022.11.07 |
|---|---|
| 복잡도 (0) | 2022.11.07 |
| Unfold Recursion (0) | 2021.04.15 |
| Divide and Conquer Algorithm (0) | 2021.04.14 |
| Climbing Stairs를 recursive 아닌 방법으로 풀어보기 (0) | 2021.04.13 |