요약
재귀함수를 사용해서 풀면 비효율적인 호출이 많아진다. -> 다이나믹 프로그래밍을 활용하자.
재귀함수로 해결할 시 시간복잡도 O(2^n)
다이나믹 프로그래밍으로 해결시 시간 복잡도 O(N)
멘토님의 키워드
왜 n은 30까지로 해놨을까?
30이 넘으면 어떻게 되는지 돌려보기. -> overflow?!
n이 30, 50, 100, 500일때 구해보기.
구글에 int32 range, unsigned int32 range 등으로 검색하면
Type Name Bytes Range of Values
__int32 4 -2,147,483,648 to 2,147,483,647
unsigned __int32 4 0 to 4,294,967,295
__int64 8 -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807
unsigned __int64 8 0 to 18,446,744,073,709,551,615
-> 음수포함 값을 unsigned일 경우 양수에 포함시켜 범위의 확장
멘토님 말씀대로 n값 30이상으로 넣어보기
fibo(50)
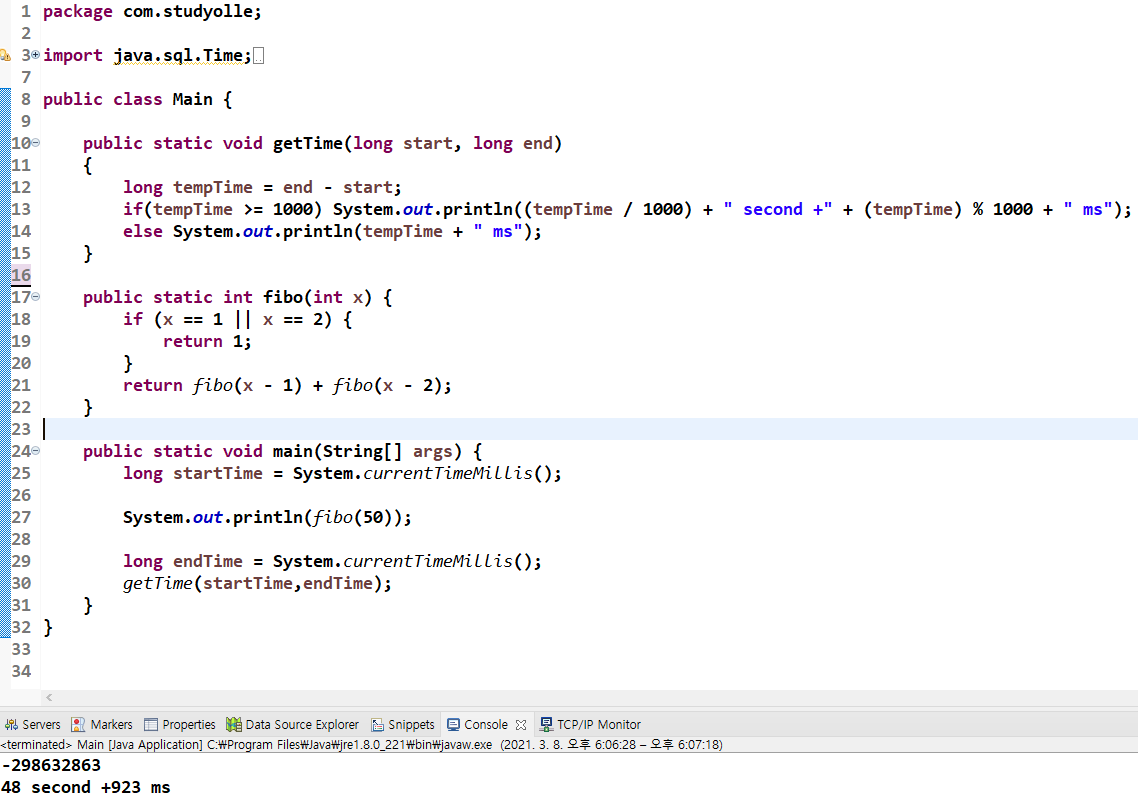
음수값이 나와서 피보나치 수열 계산기가 있어서 그 값을 가져왔더니 12,586,269,025라고 한다.
-> int범위 초과(2,147,483,647 < 12,586,269,025)
-> long이나 BigInt를 사용하면 되지 않을까...
fibo(52)
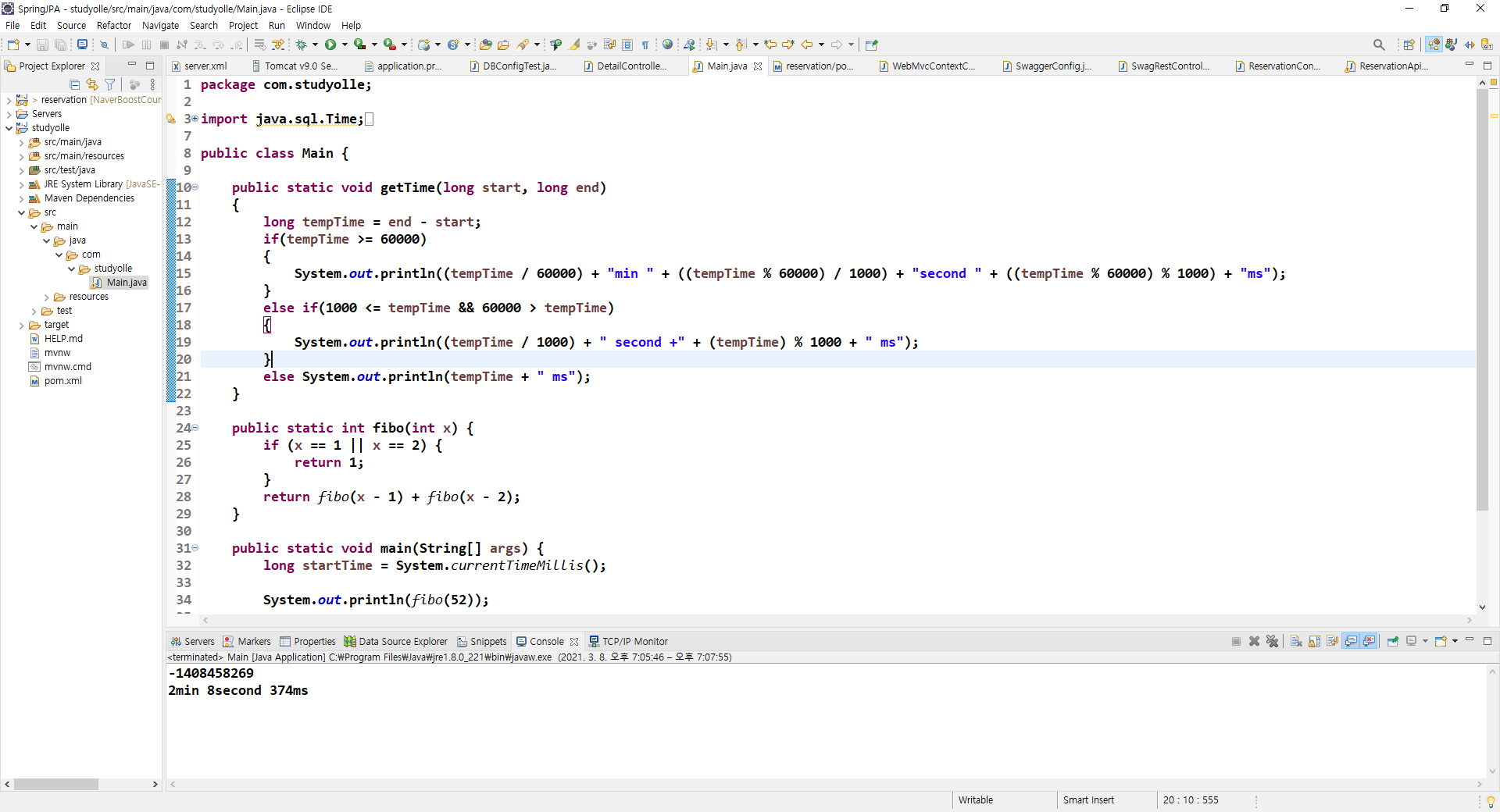
100과 60을 시도했다가 밥을 하고 먹고 와도 여전히 실행중이어서 스크린샷을 포기한 것은 안 비밀
fibo(500)
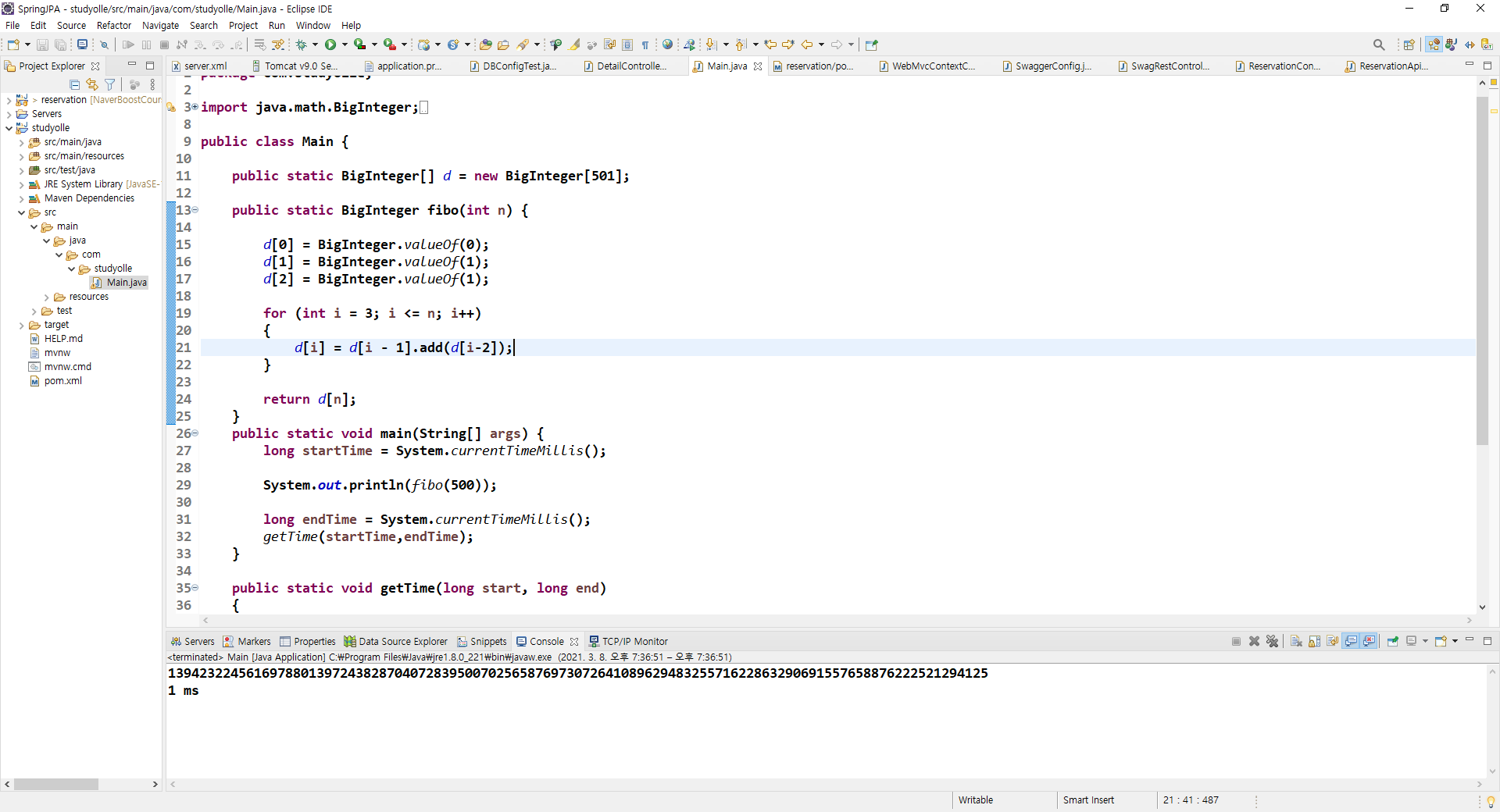
n이 30, 50, 100일때 실행시간은?
n이 6라고 가정해보자
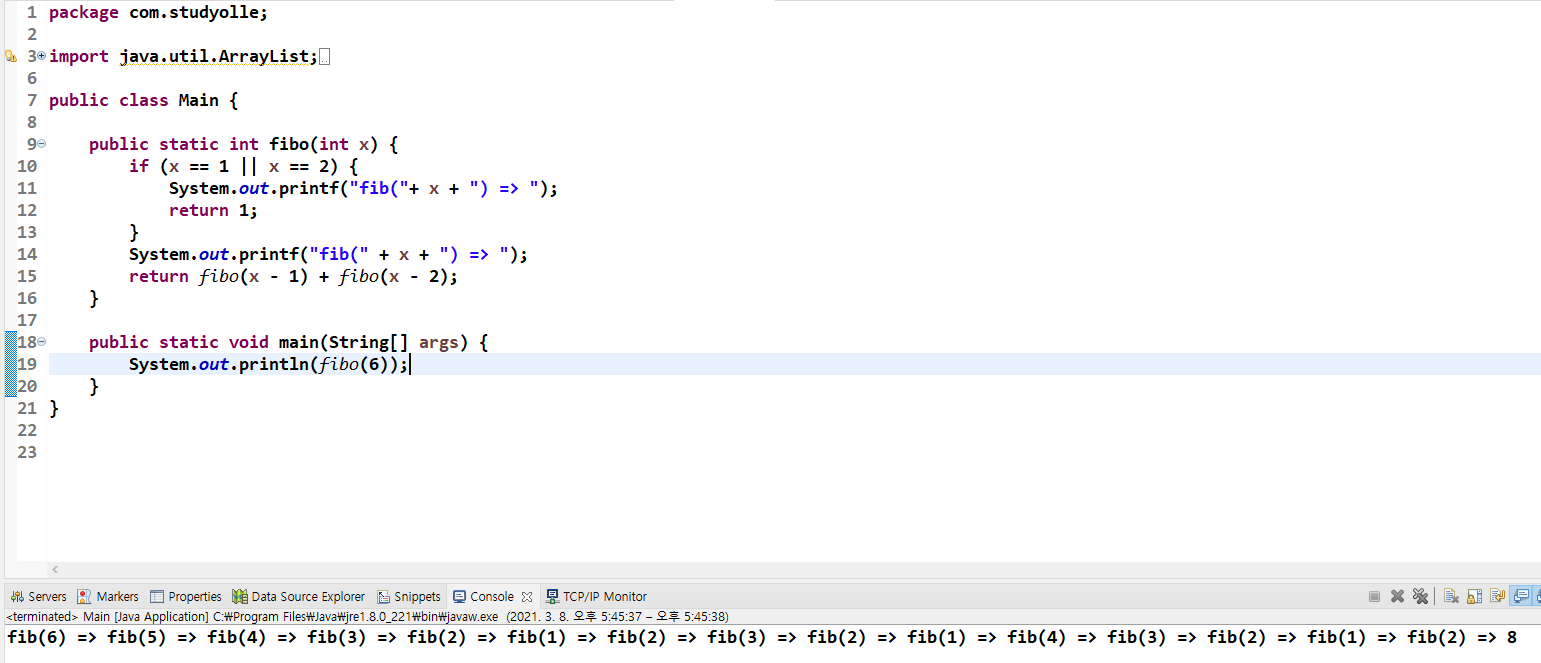
동일한 함수가 반복적으로 호출된다. f(3)은 3번 호출 되었다. n값이 커질수록 반복 호출도 매우 많아진다.
피보나치 수열의 정확한 시간복잡도는 세타 표기법으로 Θ(1.618...^n)
일반적인 빅오 표기법은 O(2^n)의 지수 시간이 필요하다.
이는 n이 30일 경우 약 10억가량의 연산을 수행해야 하고
n이 100일 경우 1,267,650,600,228,229,401,496,703,205,376 약 1,000,000,000,000,000,000,000,000,000,000번이다.
1초에 1억번 연산을 하더라도 수백억 년을 넘어간다. (100,000,000) == 1억
동빈나님의 이것이 취업을 위한 코딩테스트다 with 파이썬 내용
동빈나님의 이것이 취업을 위한 코딩테스트다 with 파이썬의 다이나믹 프로그래밍 챕터의 일부 내용 발췌
이를 해결하기 위해 다이나믹 프로그래밍이 도입된다.
다이나믹 프로그래밍은 다음 조건을 만족할 때 사용할 수 있다.
1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 동일하다.
피보나치 수열은 이러한 조건을 만족하는 대표 문제이다.
거기에다 메모이제이션(Memoization) 기법을 사용해서 해결해보자.
메모이제이션은 다이나믹 프로그래밍을 구현하는 방법의 한 종류로, 한번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법을 의미한다. 메모이제이션은 값을 저장하는 방법이므로 캐싱(Caching)이라고도 한다.
그렇다면 메모이제이션은 어떻게 구현될 수 있는가? -> 단순하다! 한 번 구한 정보를 리스트에 저장하는 것이다.
java에서는 static을 통해 언제든 접근할 수 있도록 하자.
다이나믹 프로그래밍과 퀵 정렬은 큰 문제를 작은 문제로 나누는 것에 있어 결이 비슷하다.
-> 분할 정복 알고리즘 (Divide and Conquer Algoritm)
서로의 차이점은 다이나믹 프로그래밍은 문제들이 서로 영향을 미치고 있다는 점이다.
퀵 정렬은 한번 기준 원소(Pivot)가 자리를 변경해서 자리를 잡게 되면,
그 기준 원소의 위치는 더 이상 바뀌지 않고 그 피벗값을 다시 처리하는 부분 문제는 존재하지 않는다.
반면 다이나믹 프로그래밍은 한번 해결했던 문제를 다시금 해결한다는 점이 특징이다.
그렇기에 이미 푼 문제를 배열에 저장해 놓고 이 문제는 해결 했던 것이니 다시 해결할 필요가 없다고 반환으로 처리하는 것이다.
이를 적용하면 시간복잡도가 O(N)으로 줄어든다!
다이나믹 프로그래밍은 상향식과 하향식으로 나뉘는데 상향식은 Bottom-up 하향식은 Top-Down 방식이다.
다이나믹 프로그래밍의 전형적인 형태는 Bottom-up 방식이다.
Bottom-up 방식에서 사용되는 저장용 리스트는 'DP 테이블'이라고 부르며, 메모이제이션은 탑다운 방식에 국한되어 사용되는 표현이다.
(메모이제이션은 이전에 계산된 결과를 일시적으로 기록해 놓은 넓은 개념을 의미 != 다이나믹 프로그래밍)
가급적 보텀업 방식으로 구현을 권장 -> 시스템상 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문이다.
멘토님이 언어별 for문 사용 횟수 제한이 각각 다르게 있다는 말씀을 하셨다.
문제 풀이 순서
1. 유형 파악 (완전 탐색 알고리즘으로 접근시 시간이 매우 오래 걸리면 다이나믹 프로그래밍으로 적용할 수 있는지 해결하고자 하는 부분 문제들의 중복 여부 확인)
2. 단순 재귀함수로 비효율적인 프로그램 작성(탑 다운) -> 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면(메모이제이션 활용 여부) -> 코드 개선
개선된 코드
전에 봤던 동빈나님의 코딩테스트 책에서 봤던 다이나믹 프로그래밍 방식 - Top Down
class Solution {
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 배열 초기화
public static int[] d = new int[31];
// 피보나치 함수(Fibonacci Function)를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
public static int fib(int n) {
// 종료 조건(1 혹은 2일 때 1을 반환)
if (n == 0) return 0;
else if (n == 1 || n == 2) return 1;
// 이미 계산한 적 있는 문제라면 그대로 반환
if (d[n] != 0) {
return d[n];
}
// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[n] = fib(n - 1) + fib(n - 2);
return d[n];
}
}
Runtime: 0 ms, faster than 100.00% of Java online submissions for Fibonacci Number.
Memory Usage: 35.7 MB, less than 57.59% of Java online submissions for Fibonacci Number.
0ms
35.7 MB
마찬가지로 동빈나님의 코딩테스트 책의 다이나믹 프로그래밍 Bottom-up 방식
class Solution {
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 배열 초기화
public static int[] d = new int[31];
// 피보나치 함수(Fibonacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
public int fib(int n) {
// 0번째 피보나치 수 는 0 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[0] = 0;
d[1] = 1;
d[2] = 1;
for (int i = 3; i <= n; i++)
{
d[i] = d[i - 1] + d[i - 2];
}
return d[n];
}
}
Runtime: 0 ms, faster than 100.00% of Java online submissions for Fibonacci Number.
Memory Usage: 35.2 MB, less than 98.92% of Java online submissions for Fibonacci Number.
0ms & 35.2MB'Algorithm > LeetCode' 카테고리의 다른 글
| [LeetCode] Binary Tree Inorder TraversalSolution (0) | 2021.03.10 |
|---|---|
| [LeetCode] Divisor Game (Dynamic Programming) (0) | 2021.03.09 |
| [LeetCode] Divisor Game (0) | 2021.03.08 |
| [LeetCode] Fibonacci number (피보나치 수열) (0) | 2021.03.06 |
| [LeetCode] Sort Colors (0) | 2021.03.05 |